Vue2和Vue3的domDiff

转载于

说说 vue2 和 vue3 核心diff算法 - 掘金 (juejin.cn)

觉得很不错，记录一下。

作者：陈小边
链接：https://juejin.cn/post/7092068900589797413
来源：稀土掘金
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

命令式和声明式

命令式：代码本身描述的是“做事的过程”，在代码开发的时候，我们需要维护实现目标的整个过程，包括要手动完成DOM元素的创建、更新、删除等工作。如：Jquery就是典型的命令式框架.
声明式：更加关注结果，代码展示的就是我们要的结果，看上去更加直观，至于做事儿的过程，并不需要我们关心.
从上面可以看出声明式的可维护性高于命令式，心智负担也小于命令式，但性能比命令式要差。
命令式代码的更新性能消耗 = 直接修改的性能消耗，
声明式 = 直接修改 + 找出差异的性能消耗。
那么我们只要能把找出差异的性能消耗最小化，就可以让声明式的消耗无限接近命令式。这个时候我们就要使用虚拟dom和diff算法了

什么是虚拟DOM和diff算法

虚拟DOM就是用来表示真实dom的对象，vue通过模版编译生成虚拟DOM树，然后在通过渲染器渲染成真实DOM,当数据更新时，产生新的虚拟dom树，如果直接用新的虚拟DOM树生成真实DOM并不是最优的方法。为了进一步降低找出差异的性能的性能消耗，就要使用diff算法。Diff算法是一种对比算法。对比两者是旧虚拟DOM和新虚拟DOM，对比出是哪个虚拟节点更改了，找出这个虚拟节点，并只更新这个虚拟节点所对应的真实节点，实现精准地更新真实DOM。

注：下图示中的a,b,c为节点的key值，所有的移动插入删除操作都在真实dom，下文所讲是diff算法中的核心部分

vue2 双端diff算法的实现

vue2采用了双端diff算法。核心方法是updateChildren,通过新前与旧前、新后与旧后、新后与旧前、新前与旧后、暴力比对5种查找。
新前：newChildren中所有未处理的第一个节点
新后：newChildren中所有未处理的最后一个节点
旧前：oldChildren中所有未处理的第一个节点
旧后：oldChildren中所有未处理的最后一个节点

在具体介绍前我们还需要了解isSameVnode这个用来对比两个节点是否相同的方法

// 判断两个vnode的标签和key是否相同 如果相同 就可以认为是同一节点就地复用
function isSameVnode(oldVnode, newVnode) {
  return oldVnode.tag === newVnode.tag && oldVnode.key === newVnode.key;
}

新前与旧前

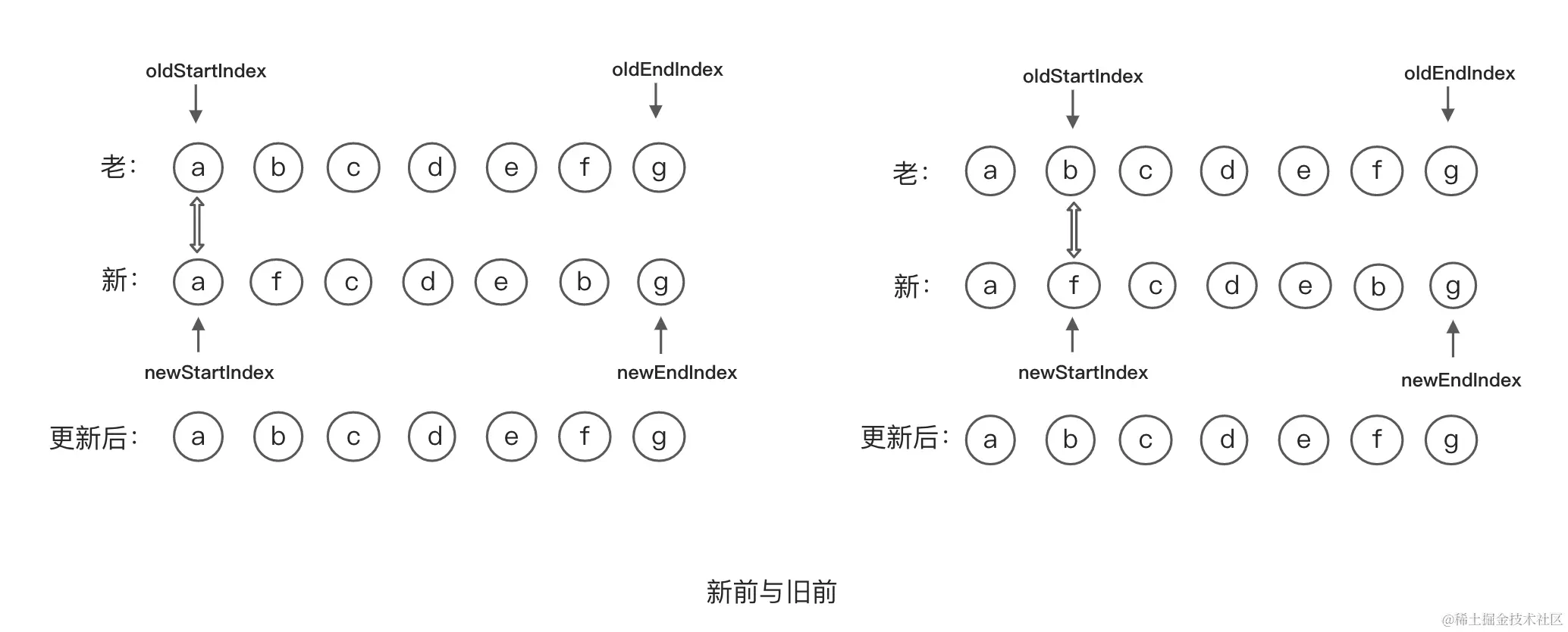
新前与旧前对比，如果相同那么新，老的开始下标往后移动一格，上图中a的新老节点相同，位置移动b位置，此时新节点为f,两节点不同，进入新后与旧后比对

新后与旧后

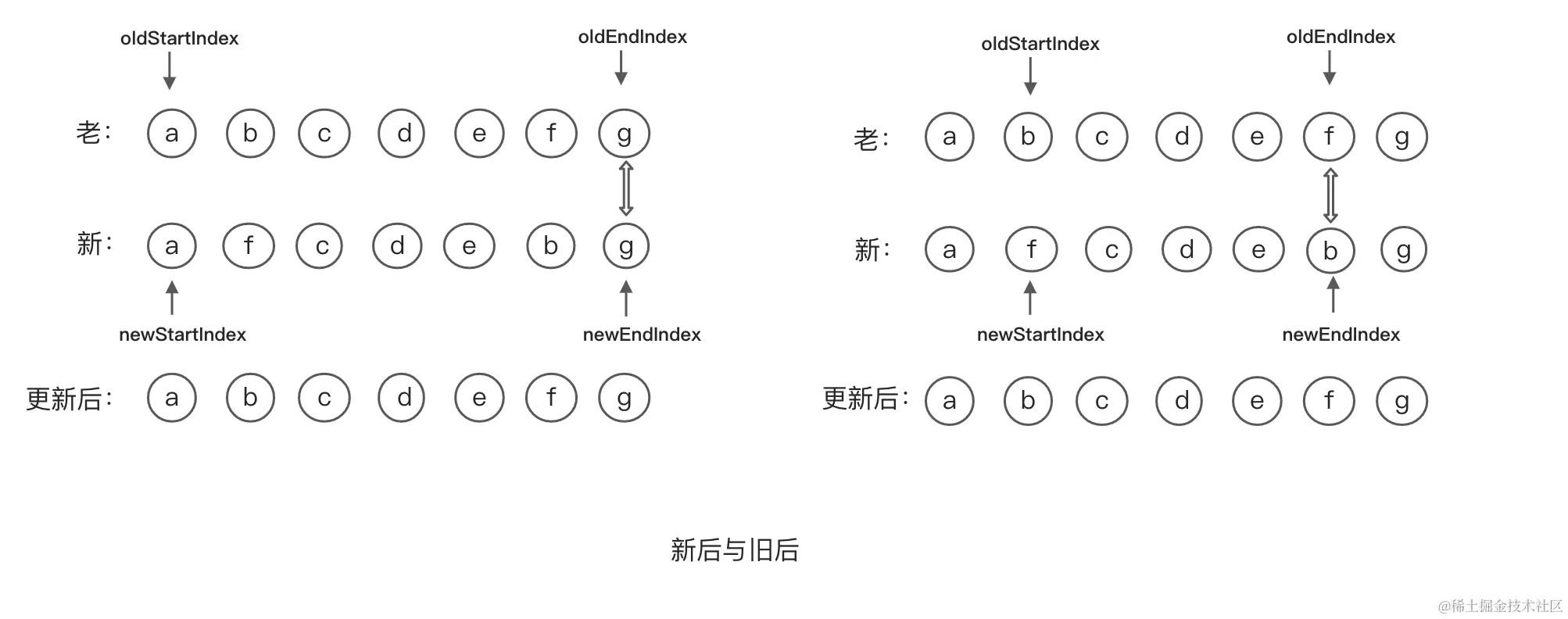
新后与旧后对比，如果相同那么新，老的结束下标往前移动一格，上图中g的新老节点相同，位置移动f位置，此时新节点为b,两节点不同，这时发现新后与旧后，新前与旧前都不满足，进入新后与旧后比对

新后与旧前

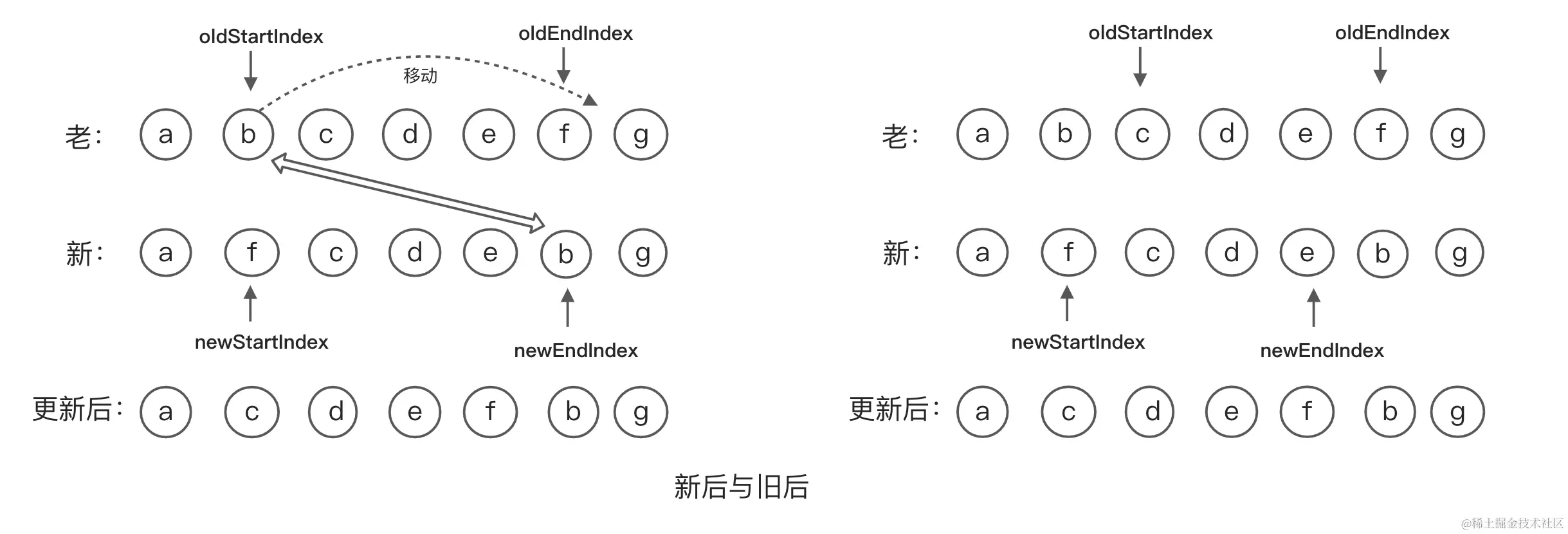新后与旧前对比，如果相同那么，把老的开始节点移动到老的结束节点后面，然后老的开始下标往后移动一格，新的结束下标往前移动一格。这时发现新的位置以上3种都不能满足，进入新前与旧后比对

新前与旧后

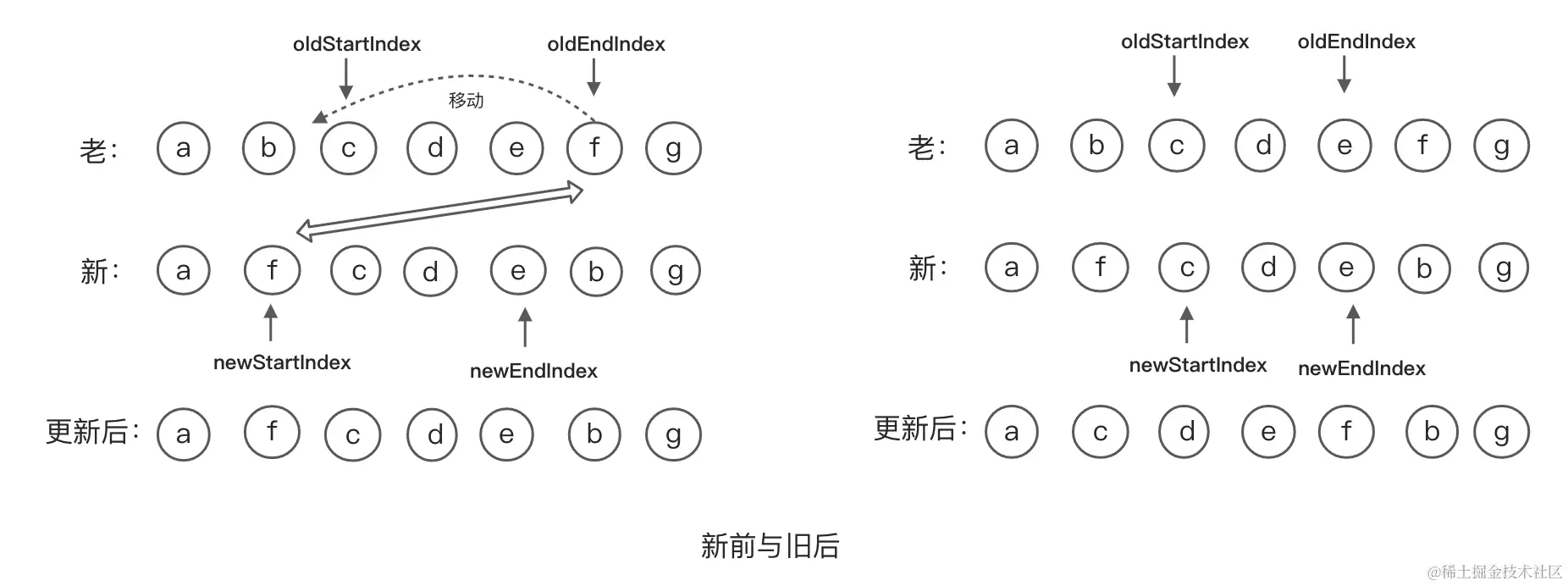新前与旧后对比，如果相同那么，把老的结束节点移动到老的开始节点前面，然后新的开始下标往后移一格，老的结束下标往前移动一格。

暴力比对(乱序)

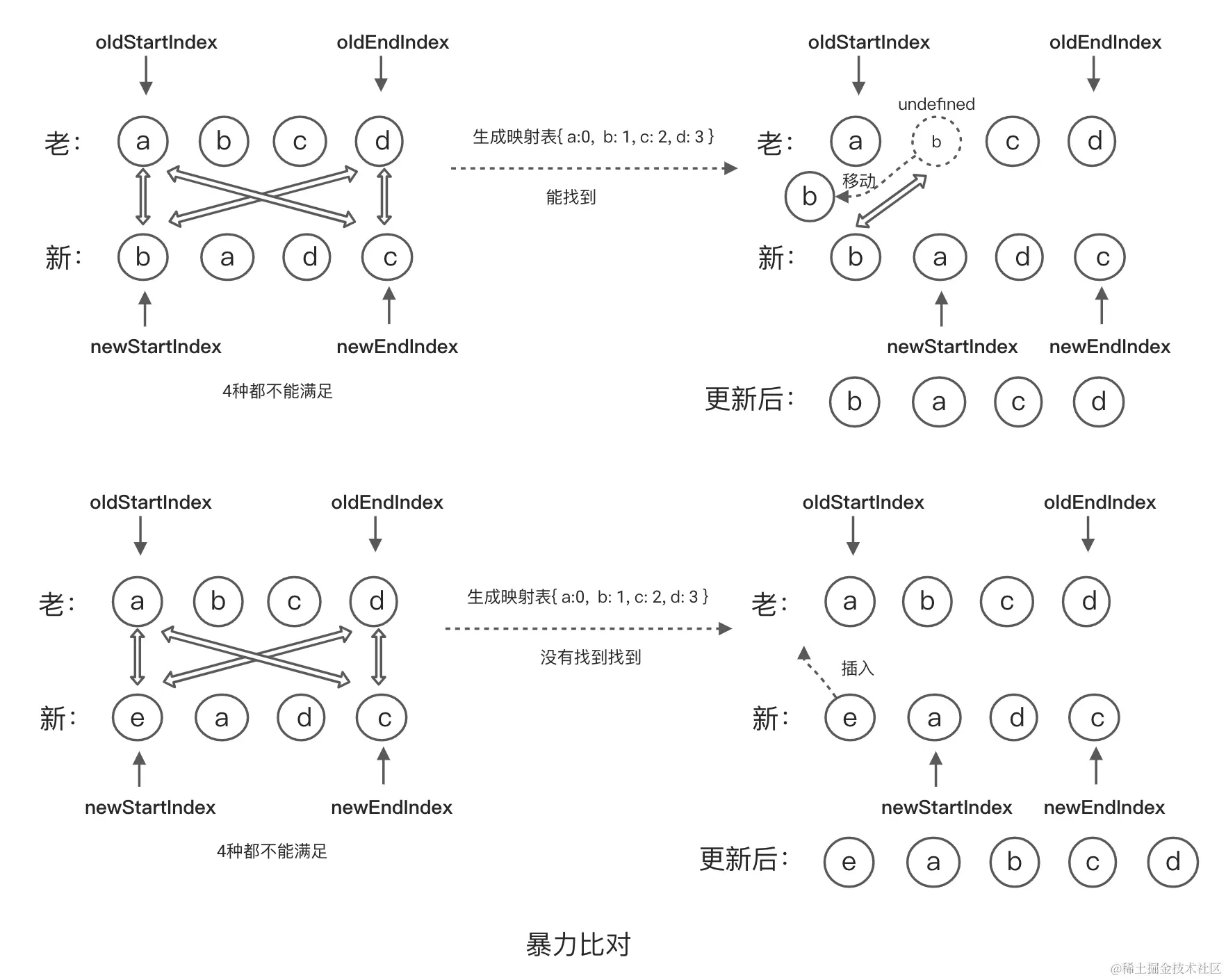
如果节点比对的时候上面4种方法都不适用时，此时我们只能用最暴力的方法，首先我们需要循环oldChildren生成一个key和index的映射表{'a': 0, 'b': 1},然后我们用新的开始节点的key,去映射表中查找，如果找到就把该节点移动到最前面，且原来的位置用undefined占位，避免数组塌陷 防止老节点移动走了之后破坏了初始的映射表位置，如果没有找到就直接把新节点插入

新节点有剩余

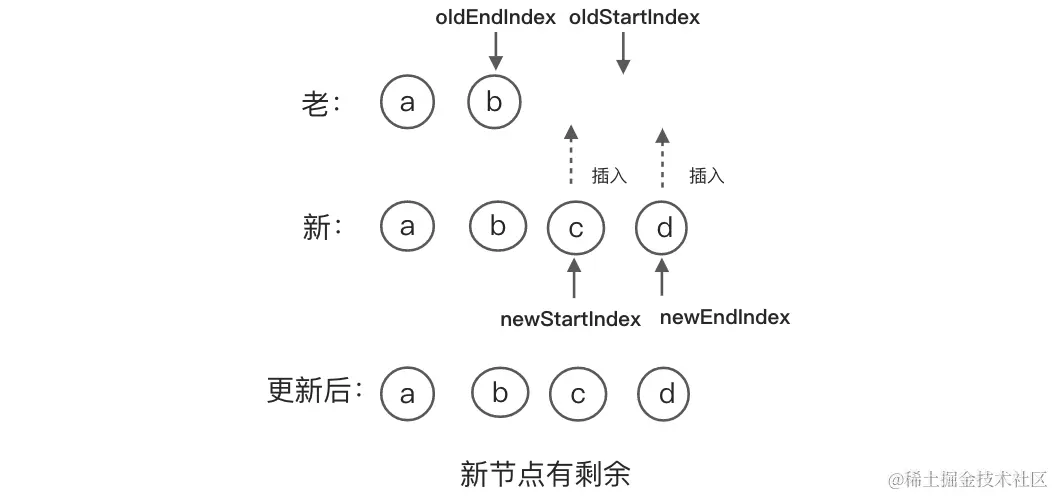有时候我们会添加新的数据，这时后上面循环结束后，newChildren还有剩余的节点还没有处理，我们需要循环这些节点，逐个插入。如上图所示。当oldStartIndex > oldEndIndex时,新的子节点还有c, d两个节点多余，需循环插入这2个节点。

老节点有剩余

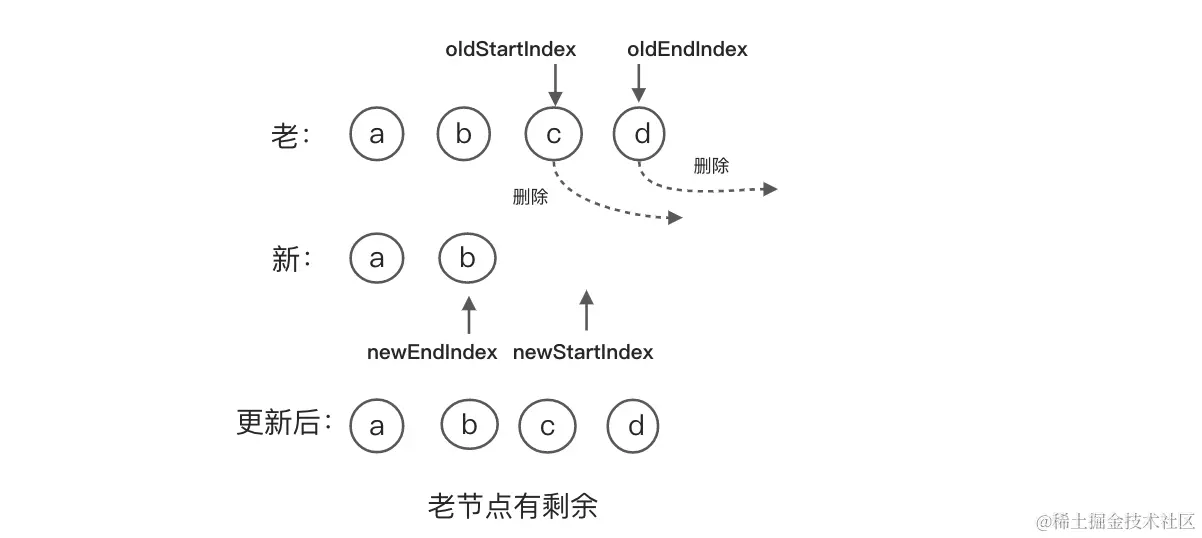另一种情况就是当我们删除元素，这时当对比循环结束后，oldChildren还有剩余的节点还没有处理，我们需循环这些节点，逐个删除。如上图所示。当newStartIndex > newEndIndex时，老的子节点还有c,d两个节点多余，循环删除这2个节点

全部核心代码

// diff算法核心 采用双指针的方式 对比新老vnode的儿子节点
function updateChildren(el, oldChildren, newChildren) {
  let oldStartIndex = 0; // 老儿子的开始下标
  let oldStartVnode = oldChildren[0]; // 老儿子的第一个节点
  let oldEndIndex = oldChildren.length - 1; // 老儿子的结束下标
  let oldEndVnode = oldChildren[oldEndIndex] // 老儿子的最后一个节点
  let newStartIndex = 0; // 新儿子的开始下标
  let newStartVnode = newChildren[0]; // 新儿子的第一个节点
  let newEndIndex = newChildren.length - 1; // 新儿子的结束下标
  let newEndVnode = newChildren[newEndIndex] // 新儿子的最后一个节点
  
  // 根据key来创建老的儿子的index映射表，如{'a': 0, 'b': 1}代表key为'a'的节点在第一个位置，'b'在第二个位置
  const makeIndexBykey = (children) => {
    return children.reduce((memo, cur, index) => {
      memo[cur.key] =  index
      return memo
    }, {})
  }
  const keysMap = makeIndexBykey(oldChildren)
  
  // 只有当新、老儿子的开始下标都小于等于结束下标时才循环，一方不满足就结束循环
  while(oldStartIndex <= oldEndIndex && newStartIndex <= newEndIndex) {
     // 因为暴力对比过程把移动的vnode置为 undefined 如果不存在节点直接跳过
    if (!oldStartVnode) { 
        // 开始位置 向后 +1
      oldStartVnode = oldChildren[++oldStartIndex]
    } else if (!oldEndVnode) {
        // 结束位置 向前 -1
      oldEndVnode = oldChildren[--oldEndIndex]
    }

    if (isSameVnode(oldStartVnode, newStartVnode)) { 
      // 新前和后前相同
      // 递归比较儿子以及他们的子节点
      patch(oldStartVnode, newStartVnode)
      // 新，老开始下标 +1， 对应的节点变为 +1 后的节点
      oldStartVnode = oldChildren[++oldStartIndex]
      newStartVnode = newChildren[++newStartIndex]
    } else if (isSameVnode(oldEndVnode, newEndVnode)) {
      // 新后和旧后相同
      // 递归比较儿子以及他们的子节点
      patch(oldEndVnode, newEndVnode)
      // 新，老结束下标 -1， 对应的节点变为 -1 后的节点
      oldEndVnode = oldChildren[--oldEndIndex]
      newEndVnode = newChildren[--newEndIndex]
    } else if (isSameVnode(oldStartVnode, newEndVnode)) { 
      // 新后和旧前相同
      // 递归比较儿子以及他们的子节点
      patch(oldStartVnode, newEndVnode)
      // 开始节点的真实dom,移动到结束节点的下一个前点的前面
      el.insertBefore(oldStartVnode.el, oldEndVnode.el.nextSibling)
      // 老的开始下标 +1， 对应的节点变为 +1 后的节点
      oldStartVnode = oldChildren[++oldStartIndex]
      // 新的结束下标 -1， 对应的节点变为 -1 后的节点
      newEndVnode = newChildren[--newEndIndex]
    } else if (isSameVnode(oldEndVnode, newStartVnode)) { 
      // 新前和旧后相同
      // 递归比较儿子以及他们的子节点
      patch(oldEndVnode, newStartVnode)
      // 结束结束的真实dom，移动到开始节点的前面
      el.insertBefore(oldEndVnode.el, oldStartVnode.el)
      // 老的结束下标 -1， 对应的节点变为 -1 后的节点
      oldEndVnode = oldChildren[--oldEndIndex]
      // 新的开始下标 +1， 对应的节点变为 +1 后的节点
      newStartVnode = newChildren[++newStartIndex]
    } else {
      // 上述四种情况都不满足 那么需要暴力比对
      // 用新的开始节点的key，去老的子节点生成的映射表中查找
      const moveIndex = keysMap[newStartVnode.key]
      if (!moveIndex) { 
        // 如果没有找到直接把新节点的真实dom，插入到旧的开始节点的真实dom前面
        el.insertBefore(createElm(newStartVnode), oldStartVnode.el)
      } else {
         // 如果找到，取出该节点
        const moveNode = oldChildren[moveIndex] 
        // 原来的位置用undefined占位 避免数组塌陷  防止老节点移动走了之后破坏了初始的映射表位置
        oldChildren[moveIndex] = undefined
        // 把取出的节点的真实dom插入到开始节点的真实dom前面
        el.insertBefore(moveNode.el, oldStartVnode.el)
        patch(newStartVnode, moveNode) //比较
      }
      // 新的开始下标 +1, 对应的节点变为 +1 后的节点
      newStartVnode = newChildren[++newStartIndex]
    }
  }
  // 如果老节点循环完毕了 但是新节点还有，如用户追加了一个，需要把剩余的节点插入
  if (newStartIndex <= newEndIndex ) {
    for (let i = newStartIndex; i <= newEndIndex; i++) {
      // 这是一个优化写法 insertBefore的第一个参数是null等同于appendChild作用
      // 看一下 结束指针的下一个元素是否存在
      let anchor = newChildren[newEndIndex + 1] == null ? null : newChildren[newEndIndex + 1].el
      el.insertBefore(createElm(newChildren[i]), anchor)
    }
  }
  // 如果新节点循环完毕了 但是老节点还有，如用户删除一个，需要把剩余的节点删除
  if (oldStartIndex <= oldEndIndex) {
    for (let i = oldStartIndex; i <= oldEndIndex; i++) {
       // 该节点不是占位节点，才做删除操作
      if (oldChildren[i] != null) {
        el.removeChild(oldChildren[i].el)
      }
    }
  }
# }

vuu2 双端diff算法流程图(放大查看)

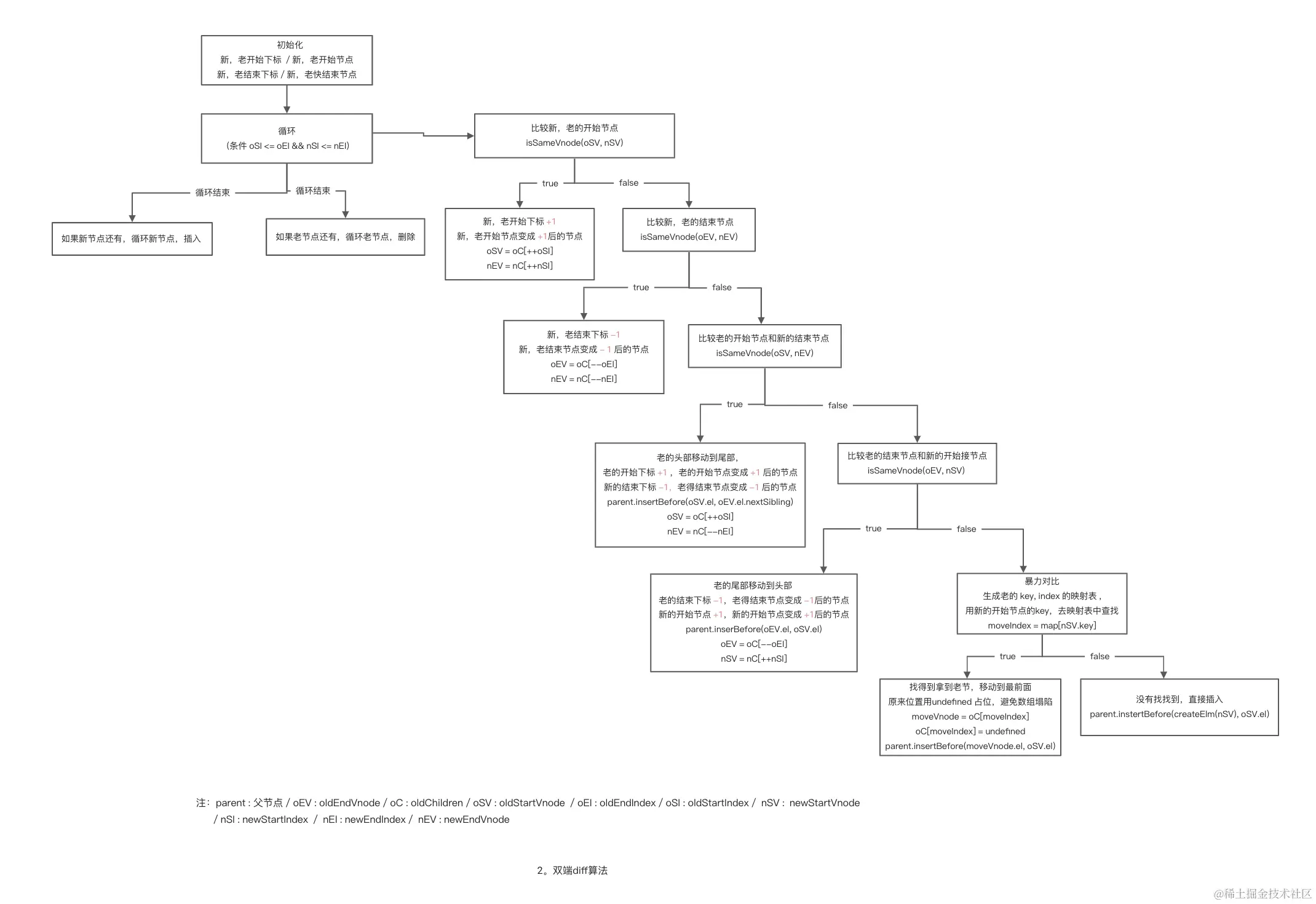
vue3 快速diff算法的实现

注：下边所讲diff算法是vuejs设计与开发书的版本，与源码版有些差别，但核心部分是一样的，可去mini-vue查看源码版

vue3 使用了快速diff算法，核心方法是patchKeyedChildren,首先是借鉴了纯文本diff算法中的预处理思路,处理新旧两个组子节点中相同的前置节点和后置节点。处理完后，如果剩余节点无法简单的通过挂载新节点或者卸载已经不存在的节点来完成更新，则需要根据节点的索引关系，构建出一个最长递增子序列。最长递增子序列所指向的节点即为不需要移动的节点。

相同前置节点处理

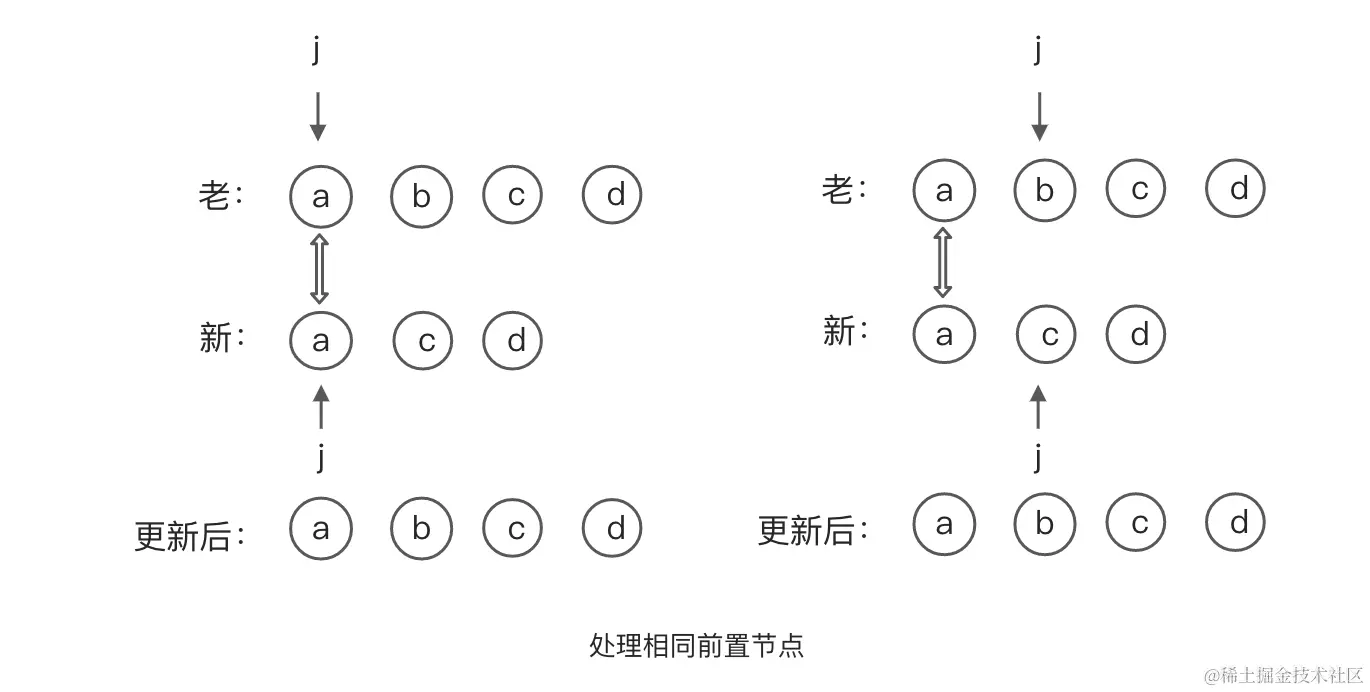
前置节点的处理是定义了一个j变量,分别指向新，老两个组子节点，比较指向的新，老节点是否相同，如果相同指针 +1,直到两个节点不同时结束前置节点的处理

相同后置节点处理

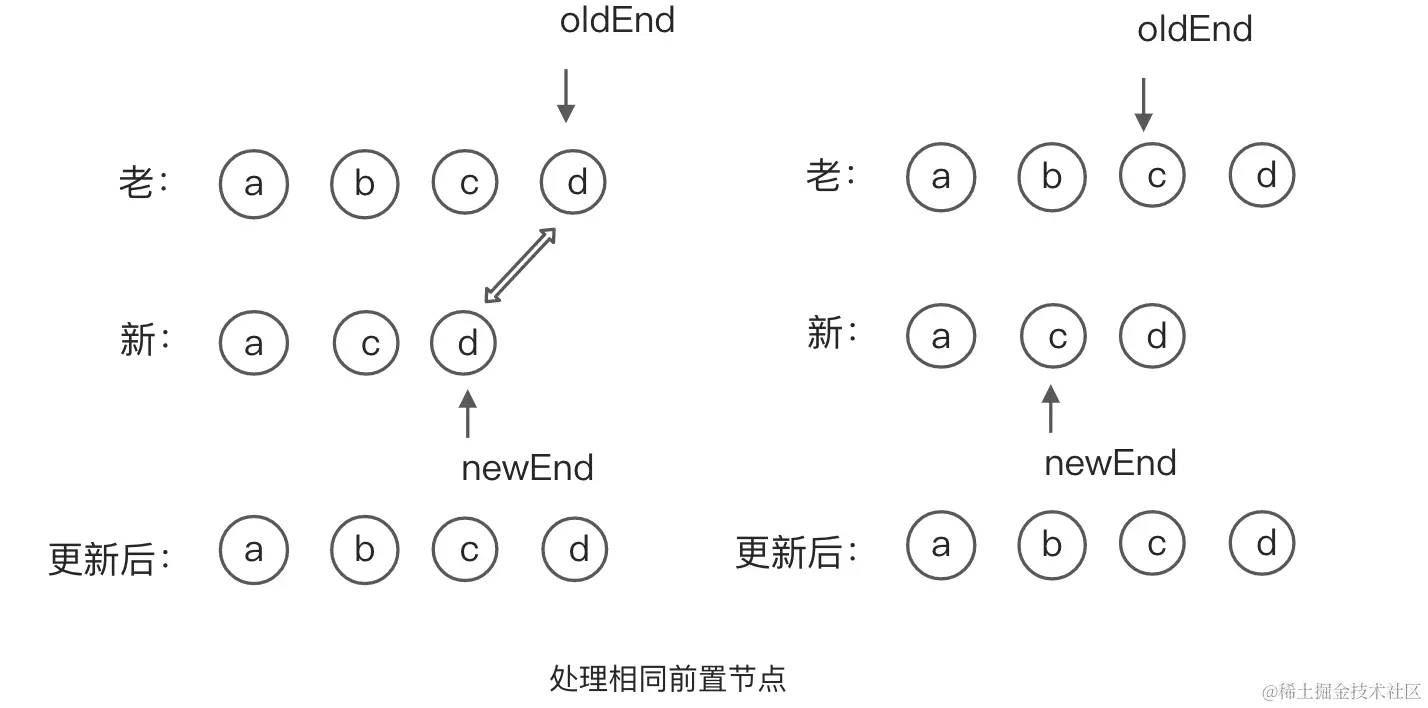
后置节点的处理是定义了索引oldEnd指向旧的一组子节点的最后一个节点和索引newEnd指向新的一组子节点的最后一个节点。然后比较两个指向的新旧节点，如果相同指向 -1，直到两个节点不同时结束后置节点的处理

剩余节点的处理

当我们处理完相同的前置节点和后置节点后，如果还有剩余节点，就要对剩余节点进行处理，剩余节点分为3中情况，分别是只有新的一组的子节点有剩余,只有老的一组的子节点有剩余,新老两组的子节点都有剩余；

只有新的一组的子节点有剩余

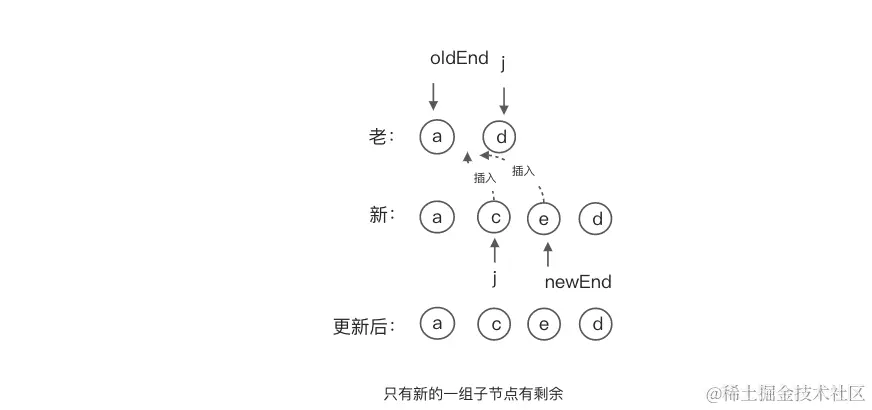
当条件满足j > oldEnd 且 j <= newEnd时，表示只有新的一组的子节点还有未处理的节点，我们需要循环 j -> newEnd中的节点进行插入

只有老的一组的子节点有剩余

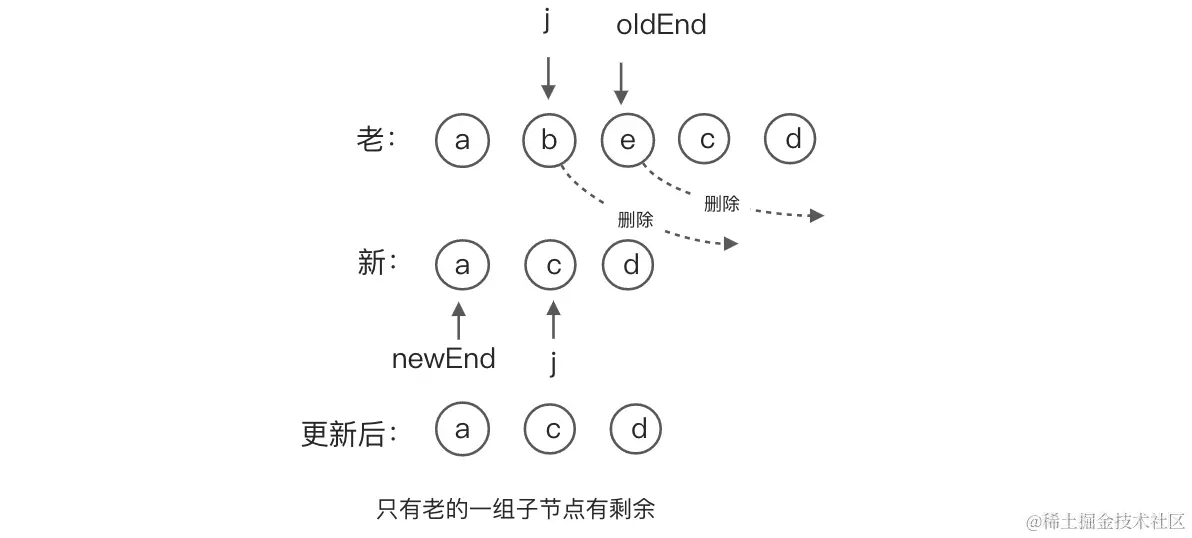当条件满足 j > newEnd 且 j <= oldEnd时，表示只有老的一组的子节点还有未处理的节点，我们需要循环 j -> oldEnd中的节点进行删除

新老两组的子节点都有剩余

该状态下主要核心为3个部分：
构建source数组用于存放新的一组子节点每个节点在老的一组中存在的原来位置(索引) 首先是定义一个长度为剩余新的一组子节点的长度的数组source，初始值都为-1，还定义了一个变量patched用于记录更新过的节点数量，然后遍历新的一组子节点，构建key与index的映射表，最后遍历老的一组节点，去映射表中寻找，k = keyIndex[oldVnode.key];，如果找到就把对应的索引存入到source对应的位置中，没有找到说明该节点多余，直接删除。

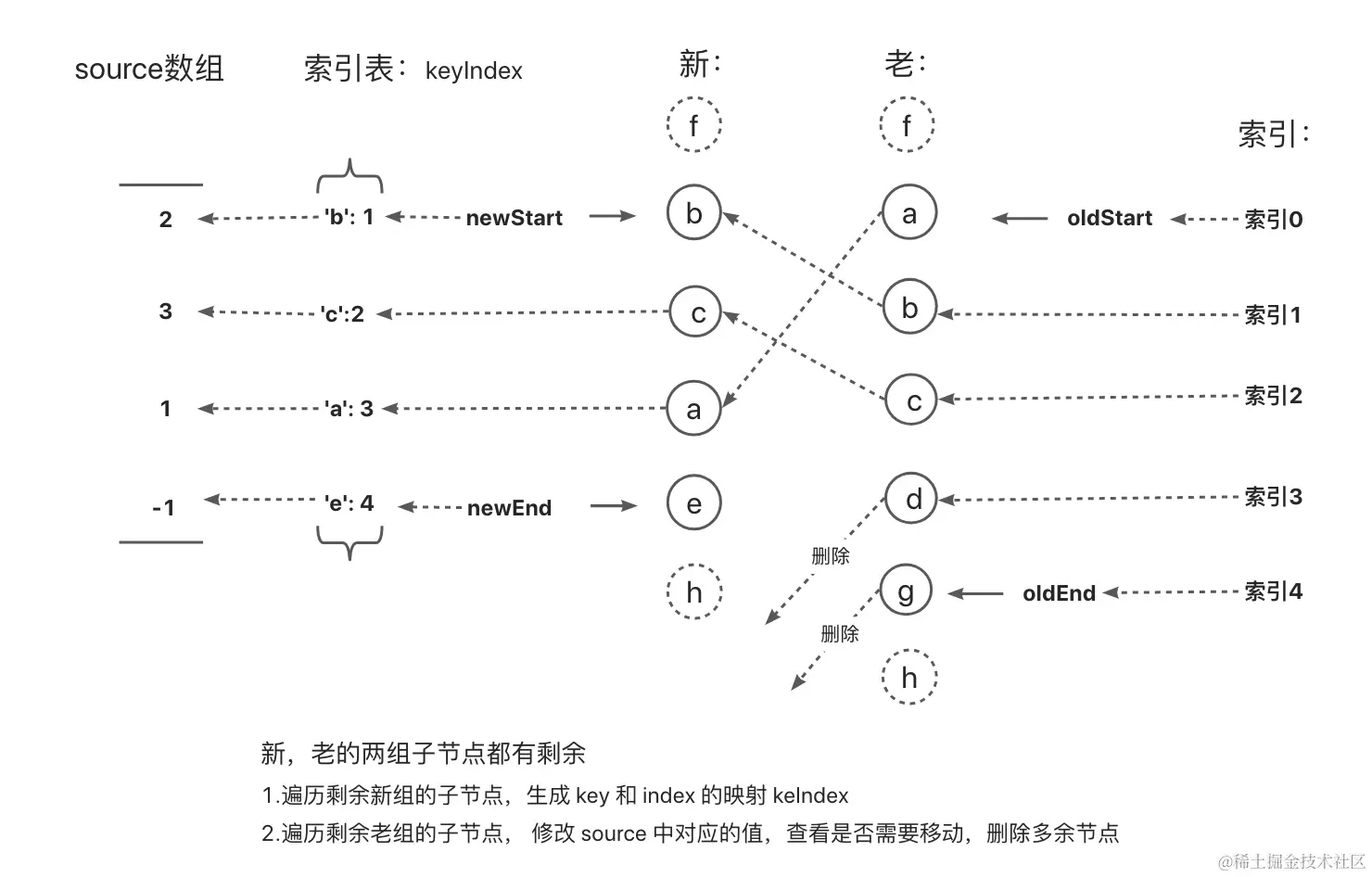
判断是否需要移动节点，首页我们会定义两个变量，moved用于记录是否需要移动的阀值,pos用于记录最后上一个节点在新组中的索引，然后用上述的k 与 pos比较，如果 k < pos,说明不是升序需要移动, 否则 pos = k

利用最长递增子序列来优化移动逻辑，如果moved = true, 首先通过最长递增子序列获取到升序列表存放的是索引，然后从后遍历新的一组节点,节点的索引与升序列表对比，如果对比上了说明不需要移动，否则需要移动。

全部核心代码

  // 获取新的子节点
  const newChildren = n2.children;
  // 获取老的子节点
  const oldChildren = n1.children;
  // 更新相同的前置节点
  // 新，老开始节点的下标
  let j = 0;
  // 获取老的一组子节点的开始节点
  let oldVnode = oldChildren[j];
  // 获取新的一组子节点的开始节点
  let newVnode = newChildren[j];
  // 如果新，老的开始节点相同
  while(oldVnode.key === newChildren.key) {
    // 递归处理子节点
    patch(oldVnode, newVnode, container);
    // 下标往后移动一格
    j++;
    // 获取 +1 后的新，老节点
    oldVnode = oldChildren[j];
    newVnode = newChildren[j];
  }
  
  // 更新相同的后置节点
  // 索引 oldEnd 指向旧的一组子节点的最后一个节点
  let oldEnd = oldChildren.length - 1;
  // 索引 newEnd 指向新的一组子节点的最后一个节点
  let newEnd = newChildren.length - 1;
  // 获取新，老结束下标对应的节点
  oldVnode = oldChildren[oldEnd];
  newVnode = newChildren[newEnd];

  // 如果新，老的结束节点相同
  while(oldVnode.key === newVnode.key) {
    // 递归处理子节点
    patch(oldVnode, newVnode, container)
    // 递减 oldEnd 和 nextEnd
    oldEnd--
    newEnd--
    // 获取递减对应的节点
    oldVnode = oldChildren[oldEnd]
    newVnode = newChildren[newEnd]
  }
  // 预处理完毕后，如果满足如下条件，则说明从 j --> newEnd 之间的节点应该作为新节点插入
  if (j > oldEnd && j <= newEnd) {
    // 锚点的索引，用于挂载时确定挂载的位置,即插入该锚点节点的前面
    const anchorIndex = newEnd + 1;
    // 锚点元素，如何anchorIndex不小于newChildren.length说明是尾部节点无需锚点元素
    const anchor = anchorIndex < newChildren.length ? newChildren[anchorIndex].el : null;
    // 采用 while 循环， 调用 patch 函数逐个挂载新增节点
    while (j <= newEnd) {
      patch(null, newChildren[j++], container, anchor)
    }
  } else if (j > newEnd && j <= oldEnd) {
    // 如果满足如下条件以上条件，那么j --> oldEnd 之间的节点应该被卸载
    while (j <= oldEnd) {
        // 循环卸载多余节点
      unmount(oldChildren[j++])
    }
  } else {
    // 获取剩余新的一组子节点的个数
    const count = newEnd - j + 1;
    // 定义个长度为 count 的 数组，用于存放新的一组子节点在老的组中位置，果然没有的话就存-1
    const source = new Array(count);
    // 初始化都存放-1
    source.fill(-1);

    // oldStart 和 newStart 分别为起始索引，即j
    const oldStart = j;
    const newStart = j;
    // 用于最后判断是否有要移动的节点
    let moved = false;
    // 遍历旧的一组子节点的过程中遇到的最大索引值 k
    let pos = 0;
    // 循环新的一组的子节点，构建key 和 index 的映射表
    const keyIndex = {};
    for(let i = newStart; i <= newEnd; i++) {
      keyIndex[newChildren[i].key] = i;
    }
    // 代表更新过的节点数量
    let patched = 0;
    // 遍历旧的一组子节点中剩余未处理的节点
    for(let i = oldStart; i <= oldEnd; i++) {
      oldVnode = oldChildren[i];
      // 如果更新过的节点数量小于等于需要更新的节点数量，则执行更新
      if (patched <= count) {
         // 取出老节点在新节点的索引
        const k = keyIndex[oldVnode.key];
        if (typeof k !== 'undefined') {
          newVnode = newChildren[k];
           // 递归处理子节点
          patch(oldVnode, newVnode, container);
          // 每更新一个节点，都将 patched 变量 +1
          patched++;
          // 存放新的一组子节点在老的组中位置 
          source[k - newStart] = i;
          // 如果该节点新的位置小于最大的索引值,说明该节点往前移了
          if (k < pos) {
            moved = true
          } else {
            // 如果不是就把该位子存到pos，目前k是递增子节点中最大的索引
            pos = k
          }
        } else {
          // 没找到, 卸载该节点
          unmount(oldVnode)
        }
      } else {
        // 如果更新过的节点数量大于需要更新的节点数量，则卸载多余的节点
        unmount(oldVnode)
      }
    }
  }
   // moved 为 true 时说明需要移动节点 
  if (moved) {
    // 计算最长递增子序列
    const seq = lis(source);
    // 最长递增子序列中最后一个值的索引
    let s = seq.length - 1;
    // 新的一组子节点从后往前遍历
    for (i = count - 1; i >=0; i--) {
         // 该节点在新 children 中的真实位置索引
        const pos = i + newStart;
        const newVnode = newChildren[pos];
        // 该节点的下一个节点的位置索引
       const nextPos = pos + 1;
        // 锚点
       const anchor = nextPos < newChildren.length ? newChildren[nextPos].el : null;
      if (source[i] === -1) {
        // 说明索引为 i 的节点是全新的节点，应该将其插入
        // 挂载
        patch(null, newVnode, container, anchor);
      } else if(s < 0 || i !== seq[s]) {
        // 如果节点的索引 i 不等于 seq[s] 的值， 说明该节点需要移动
        // s < 0 说明没有稳定的子序列(例如反向)
        // 移动
        insert(newVnode.el, container, anchor)
      } else {
        // 当 i === seq[s] 时, 说明该位置的节点不需要移动，只需要让 s 指向下一个位置
        s--
      }
    }
  }

}

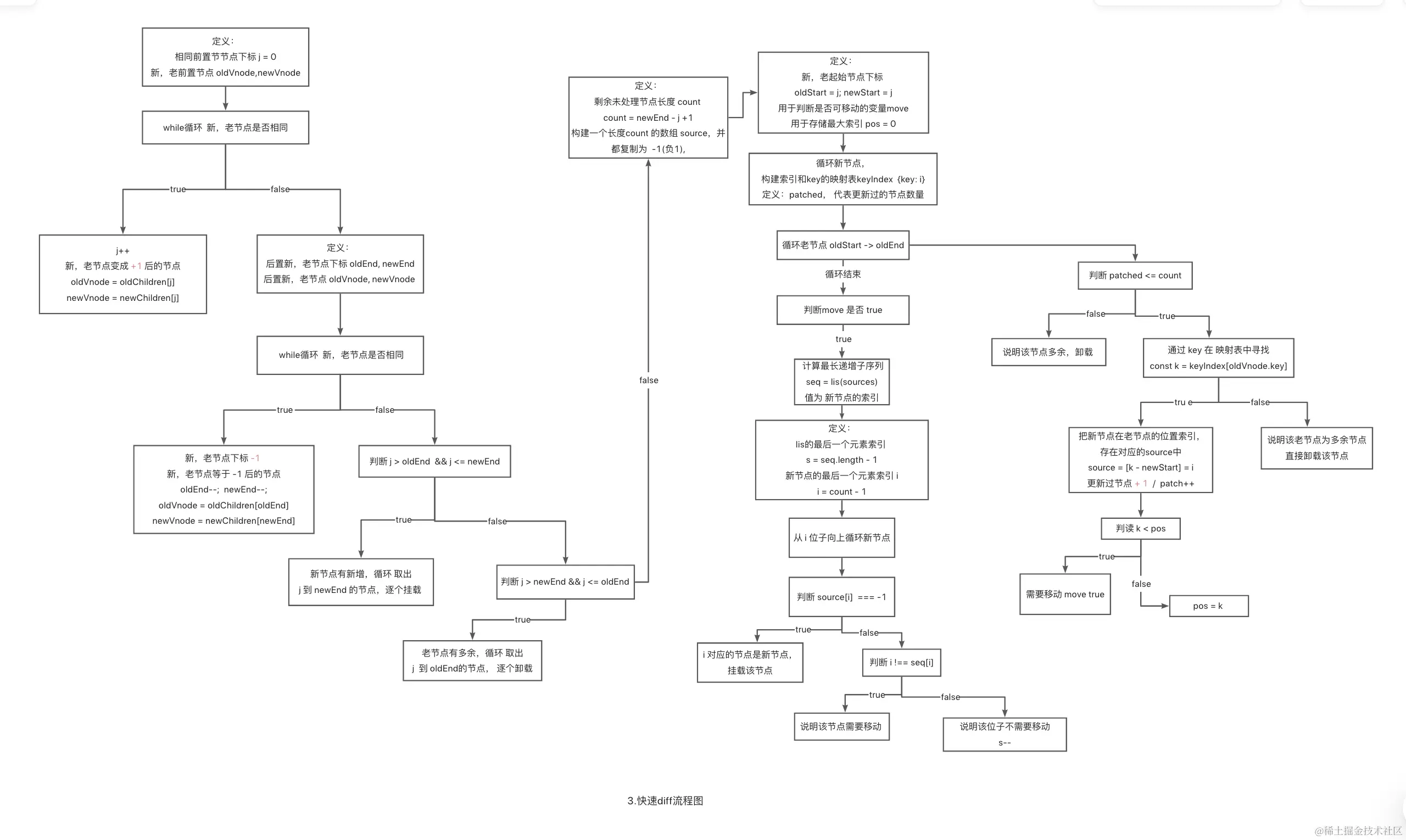
vue3 快速diff算法流程图(放大查看)